改進擴散模型以替代 GANs ，第 2 部分

這是 NVIDIA 研究人員如何改進和加速擴散模型采樣的系列文章的一部分，擴散模型是一種新的、強大的生成模型。 Part 1 介紹了擴散模型作為深層生成模型的一個強大類，并研究了它們在解決生成性學習三重困境中的權衡。

雖然擴散模型同時滿足生成性學習三位一體的第一和第二個要求，即高樣本質量和多樣性，但它們缺乏傳統 GAN 的采樣速度。在這篇文章中，我們回顧了 NVIDIA 最近開發的三種技術，它們克服了擴散模型中緩慢采樣的挑戰。

潛空間擴散模型

擴散模型的采樣速度較慢的主要原因之一是，從簡單的高斯噪聲分布到具有挑戰性的多模態數據分布的映射非常復雜。最近， NVIDIA 推出了基于潛在分數的生成模型（ LSGM ），這是一種新的框架，可以在潛在空間而不是直接在數據空間中訓練擴散模型。

在 LSGM 中，我們利用變分自動編碼器（ VAE ）框架將輸入數據映射到一個潛在空間，并在那里應用擴散模型。然后，擴散模型的任務是對數據集潛在嵌入的分布進行建模，這在本質上比數據分布更簡單。

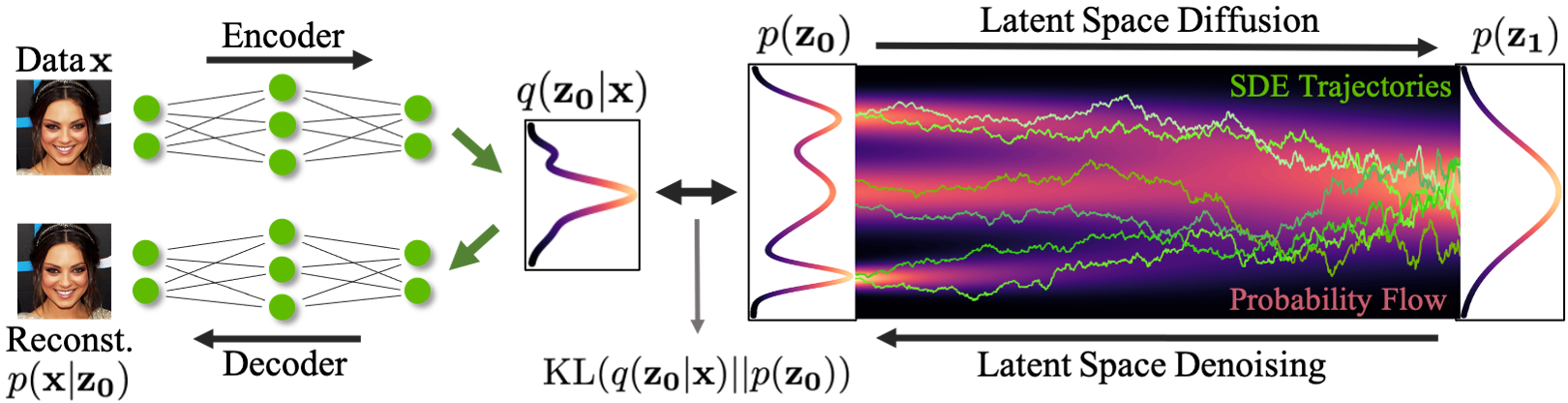
新的數據合成是通過從簡單的基分布中提取嵌入，然后迭代去噪，然后使用解碼器將該嵌入轉換為數據空間來實現的（圖 1 ）。

The data and latent spaces are mapped to each other using autoencoders. A diffusion model is formed on the latent encoding of the data. — *圖 1 。基于潛在分數的生成模型*

圖 1 顯示，在基于潛在分數的生成模型（ LSGM ）中：

數據 $\bf{x}$ 通過編碼器 $q(\bf{z}_0|\bf{x})$ 映射到潛在空間。
擴散過程應用于潛在空間 $(\bf{z}_0 \rightarrow \bf{z}_1)$ 。
合成從堿基分布 $p(\bf{z}_1)$ 開始。
它通過去噪 $(\bf{z}_0 \leftarrow \bf{z}_1)$ 在潛在空間生成樣本 $\bf{z}_0$ 。
使用解碼器 $p(\bf{x}|\bf{z}_0)$ 將樣本從潛在空間映射到數據空間。

LSGM 有幾個關鍵優勢：合成速度、表現力，以及定制的編碼器和解碼器。

合成速度

通過先用高斯先驗對 VAE 進行預訓練，可以使數據分布的潛在編碼接近高斯先驗分布，這也是擴散模型的基本分布。擴散模型只需對剩余的不匹配進行建模，從而形成一個簡單得多的模型，從中采樣變得更容易、更快。

可以相應地調整潛在空間。例如，我們可以使用分層潛變量，并僅在其中的一個子集上或以較小的分辨率應用擴散模型，從而進一步提高合成速度。

表現力

訓練一個規則的擴散模型可以看作是直接在數據上訓練一個神經網絡。然而，之前的研究發現，用潛在變量增強神經微分方程以及其他類型的生成模型通常可以提高它們的表達能力。

我們期望通過將擴散模型與潛在變量框架相結合，獲得類似的表現力收益。

定制編碼器和解碼器

在潛在空間中使用擴散模型時，可以使用精心設計的編碼器和解碼器在潛在空間和數據空間之間映射，進一步提高合成質量。因此， LSGM 方法可以自然地應用于非連續數據。

原則上， LSGM 可以通過使用編碼器和解碼器網絡，輕松地對文本、圖形和類似的離散或分類數據類型等數據進行建模，這些網絡將這些數據轉換為連續的潛在表示并返回。

直接對數據進行操作的常規擴散模型無法輕松對此類數據類型進行建模。標準擴散框架僅適用于連續數據，這些數據可以逐漸擾動并以有意義的方式生成。

后果

在實驗上， LSGM 在 CIFAR-10 和 CelebA-HQ-256 這兩個廣泛使用的圖像生成基準數據集上實現了最先進的 Fr é chet Inception 距離（ FID ），這是量化視覺圖像質量的標準度量。在這些數據集上，它優于先前的生成模型，包括 GANs 。

在 CelebA-HQ-256 上， LSGM 的合成速度比以前的擴散模型快兩個數量級。在對 CelebA-HQ-256 數據建模時， LSGM 只需要 23 次神經網絡調用，而之前在數據空間上訓練的擴散模型通常依賴數百次或數千次網絡調用。

視頻 1 。隨機遍歷 LSGM 潛在空間生成的序列

臨界阻尼朗之萬擴散

擴散模型中的一個關鍵因素是固定前向擴散過程，以逐漸擾動數據。與數據本身一起，它唯一地決定了去噪模型學習的難度。因此，我們能否設計一種特別容易去噪的前向擴散，從而實現更快、更高質量的合成？

擴散模型中使用的擴散過程在統計學和物理學等領域得到了很好的研究，它們在各種抽樣應用中都很重要。受這些領域的啟發，我們最近提出了臨界阻尼朗之萬擴散（ CLD ）。

在 CLD 中，必須擾動的數據與可被視為 velocities 的輔助變量耦合，這與物理學中的速度相似，因為它們基本上描述了數據向擴散模型的基本分布移動的速度。

就像一個落在山頂上的球，在相對直接的路徑上迅速滾動到山谷中，積累一定的速度，這種受物理啟發的技術有助于數據快速平穩地擴散。描述 CLD 的正向擴散 SDE 如下所示：

$\dbinom{d \bf{x}_t}{d \bf{v}_t} = \underbrace{ \dbinom{M^{1} \bf{v}_t}{\bf{x} t} \beta dt}_{\textrm{Hamiltonian~component} =: \it{H}} + \underbrace{ \dbinom{ \bf{0} d}{-\Gamma M^{-1}\bf{v}_t} \beta dt + \dbinom{0}{\sqrt{2 \Gamma \beta}} d \bf{w}_t}_{\textrm{Ornstein-Uhlenbeck~process} =: \it{O}}$

這里， $\bf{x}_t$ 表示數據， $\bf{v}_t$ 表示速度。 $M$ 、 $\Gamma$ 和 $\beta$ 是決定擴散以及速度和數據之間耦合的參數。 $d\bf{w}_t$ 是一個高斯白噪聲過程，負責噪聲注入，如公式所示。

CLD 可以解釋為兩個不同術語的組合。首先是一個 Ornstein-Uhlenback 過程，這是一種特殊的噪聲注入過程，作用于速度變量 $\bf{v}_t$ 。

其次，在哈密頓動力學中，數據和速度相互耦合，因此注入速度的噪聲也會影響數據 $\bf{x}_t$ 。哈密頓動力學提供了物理系統力學的基本描述，比如前面提到的例子中滾下山的球。

圖 2 顯示了一個簡單的一維玩具問題的數據和速度如何在 CLD 中擴散：

Visualization of critically-damped Langevin diffusion run in the joint data-velocity space using 1D toy distributions. — 圖 2 。在嚴重阻尼的朗之萬擴散中，數據 x_T增加了速度 v_T.擴散耦合 x_T和 v_T在聯合數據速度空間中運行（紅色表示概率）。噪聲只注入 v_T.這將導致數據 x 的平滑擴散軌跡（綠色）_T.

在擴散開始時，我們從簡單的高斯分布中提取一個隨機速度，然后在聯合數據速度空間中進行完全擴散。當觀察數據的演變（圖中右下角）時，模型的擴散方式比之前的擴散方式要平滑得多。

直觀地說，這也應該使去噪和反轉生成過程更容易。我們只在擴散參數 $M$ 和 $\Gamma$ 的特定選擇下獲得這種行為，特別是 $\Gamma^2 = 4M$ 。這種結構在物理學上被稱為臨界阻尼，對應于更廣泛的隨機動力系統 Langevin dynamics 的一個特例，因此被稱為臨界阻尼 Langevin 擴散。

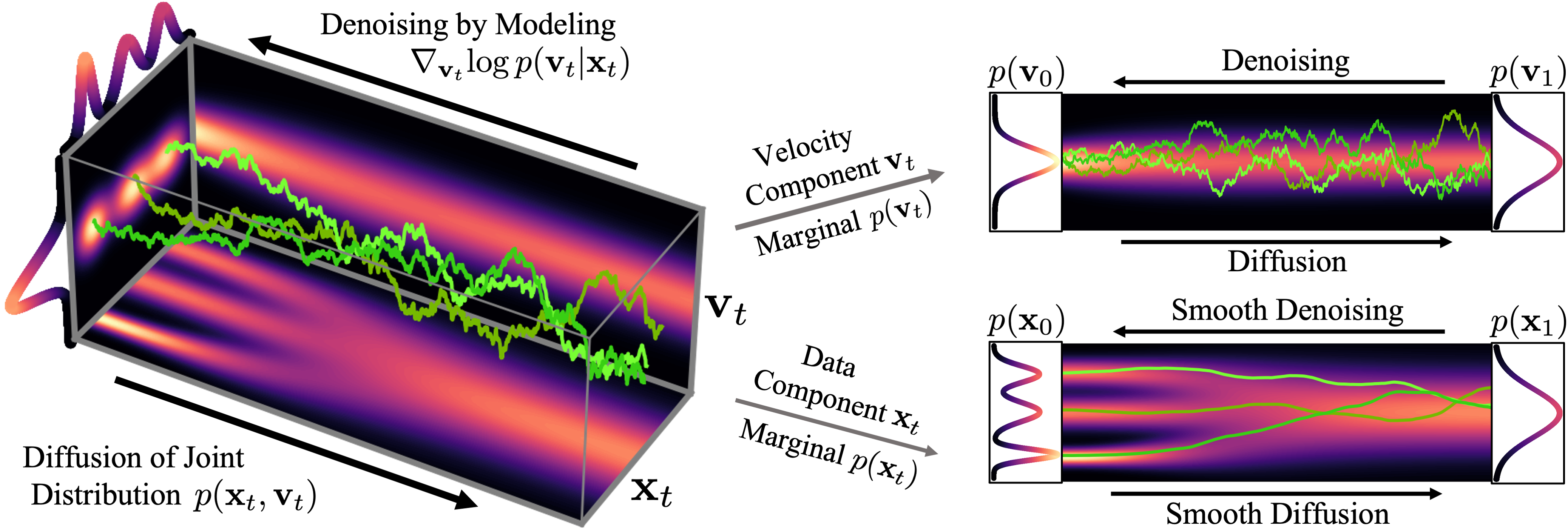
我們還可以可視化圖像在正向擴散和生成期間如何在高維聯合數據速度空間中演化：

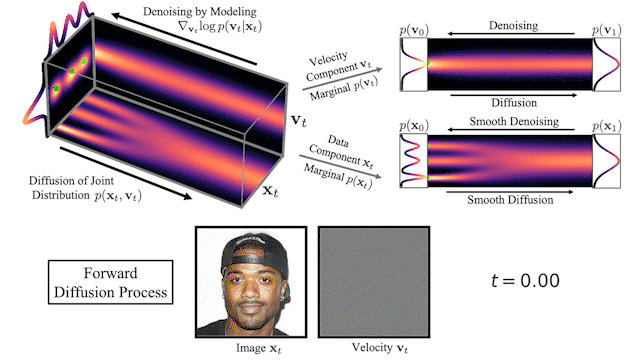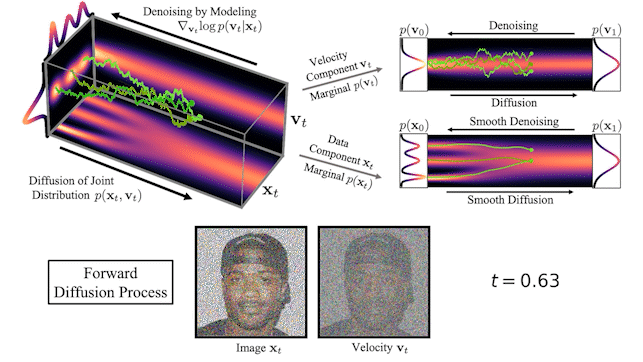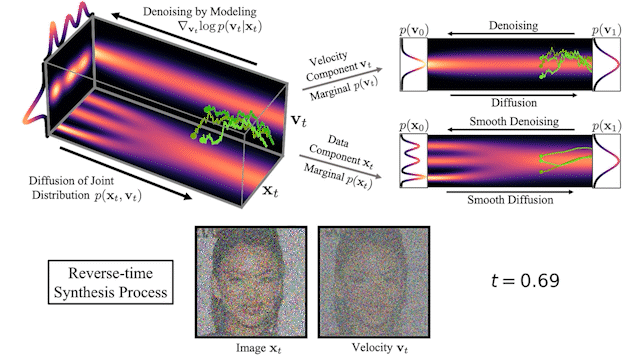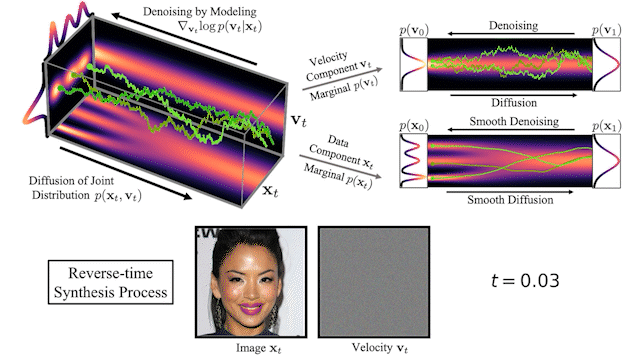
Animation of critically-damped Langevin diffusion’s forward diffusion and reverse-time synthesis processes. — F *圖 3 。 CLD 的正向擴散和反向時間合成過程*

在圖 3 的頂部，我們可視化了一維數據分布和速度如何在聯合數據速度空間中擴散，以及生成如何以相反的方向進行。我們對三種不同的擴散軌跡進行了采樣，并在右側顯示了到數據和速度空間的投影。在底部，我們將相應的擴散和合成過程可視化，以生成圖像。我們看到速度在中間時間對數據進行“編碼” $t$ 。

在培訓生成性擴散模型時使用 CLD 有兩個關鍵優勢：

更簡單的評分函數和培訓目標
使用定制 SDE 解算器加速采樣

更簡單的評分函數和培訓目標

在常規擴散模型中，神經網絡的任務是學習擴散數據分布的得分函數 $\nabla_{\bf {x}t} log ~p_t (\bf{x}_t)$ 。相比之下，在基于 CLD 的模型中，我們的任務是學習 $\nabla{\bf {v}_t} log ~p_t (\bf{v}_t|\bf{x}_t)$ ，即給定數據的速度的條件分數函數。這是只向速度變量中注入噪聲的結果。

然而，由于速度總是遵循比數據本身更平滑的分布，這是一個更容易學習的問題。基于 CLD 的擴散模型中使用的神經網絡可以更簡單，同時仍能實現較高的生成性能。與此相關，我們還可以針對基于 CLD 的擴散模型制定改進的、更穩定的訓練目標。

使用定制 SDE 解算器加速采樣

要集成 CLD 的反向時間合成 SDE ，可以導出定制的 SDE 解算器，以便對 CLD 中產生的更平滑的正向擴散進行更有效的去噪。這會加速合成。

在實驗上，對于廣泛使用的 CIFAR-10 圖像建模基準，對于類似的神經網絡結構和采樣計算預算， CLD 在合成質量上優于以前的擴散模型。此外， CLD 為生成性 SDE 量身定制的 SDE 解算器在生成速度方面明顯優于 Euler – Maruyama 等解算器，后者是一種解決擴散模型中 SDE 的常用方法。有關更多信息，請參閱基于分數的臨界阻尼朗之萬擴散生成模型。

CIFAR-10 images generated by a diffusion model based on critically-damped Langevin diffusion. — *圖 4 。由基于臨界阻尼朗之萬擴散的擴散模型生成的合成 CIFAR-10 圖像。*

我們已經證明，只要仔細設計固定正向擴散過程，就可以改進擴散模型。

擴散算子去噪

到目前為止，我們已經討論了如何通過將訓練數據移動到平滑的潛在空間（如 LSGM ）來加速擴散模型的采樣，或者通過使用輔助速度變量來增加數據，以及設計改進的前向擴散過程（如基于 CLD 的擴散模型）。

然而，加速擴散模型采樣的最直觀的方法之一是直接減少反向過程中的去噪步驟。在這一部分中，我們回到離散時間擴散模型，在數據空間中進行訓練，并分析在減少去噪步驟的數量和執行大步驟時，去噪過程的行為。?

在最近的 study 中，我們觀察到擴散模型通常假設反向合成過程中學習到的去噪分布 $p_{ \theta} (\bf{x}_{t-1}|\bf{x}_t)$ 可以近似為高斯分布。然而，眾所周知，高斯假設只適用于許多小的去噪步驟的無窮小極限，這最終導致擴散模型的合成緩慢。

當反向生成過程使用較大的步長（去噪步驟較少）時，我們需要一個非高斯、多峰分布來建模去噪分布 $p_{ \theta} (\bf{x}_{t-1}|\bf{x}_t)$ 。

直觀地說，在圖像合成中，多峰分布產生于多個看似合理且干凈的圖像可能對應于同一個噪聲圖像的事實。由于這種多模性，簡單地減少去噪步驟的數量，同時在去噪分布中保持高斯假設，會損害發電質量。

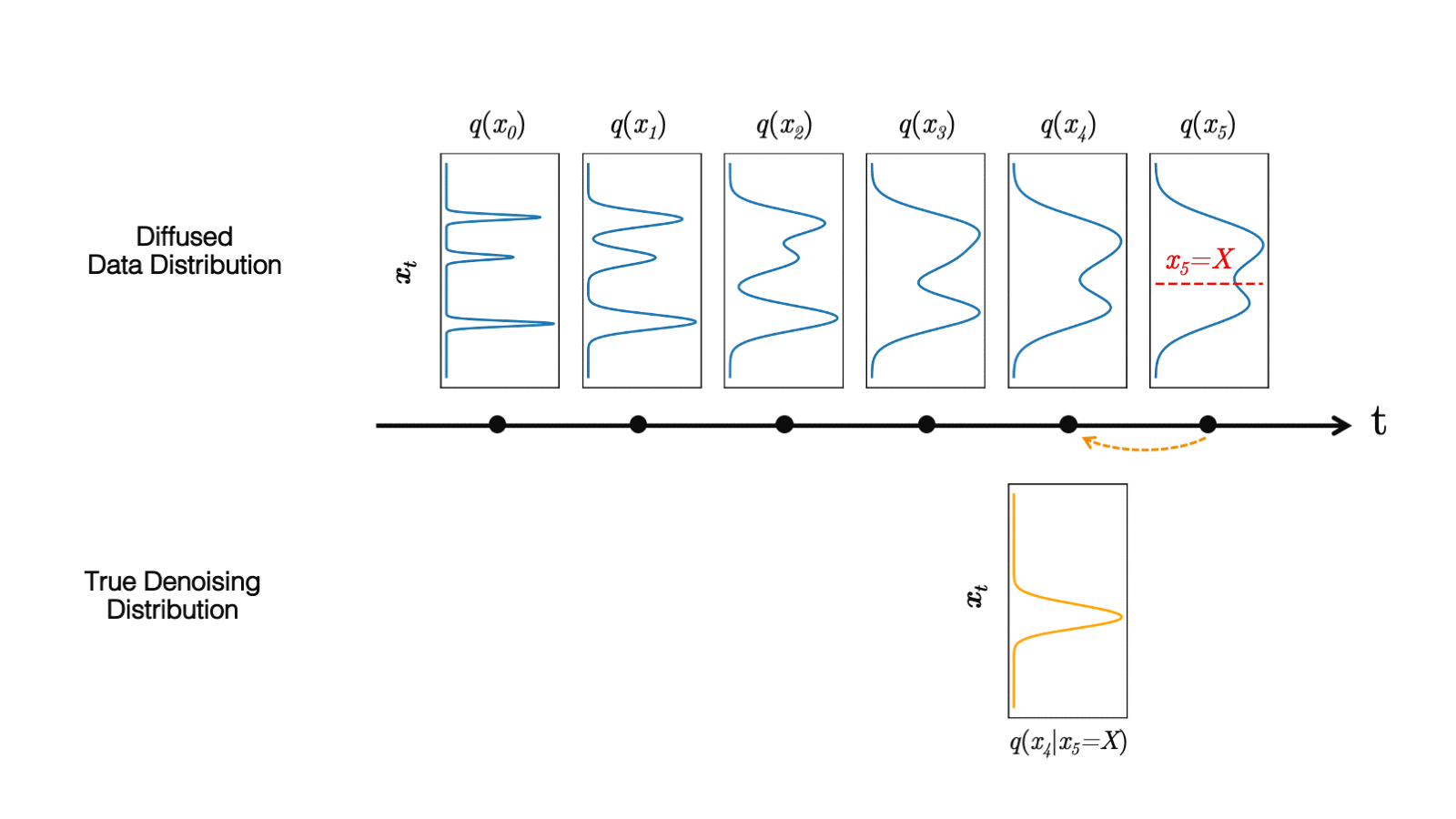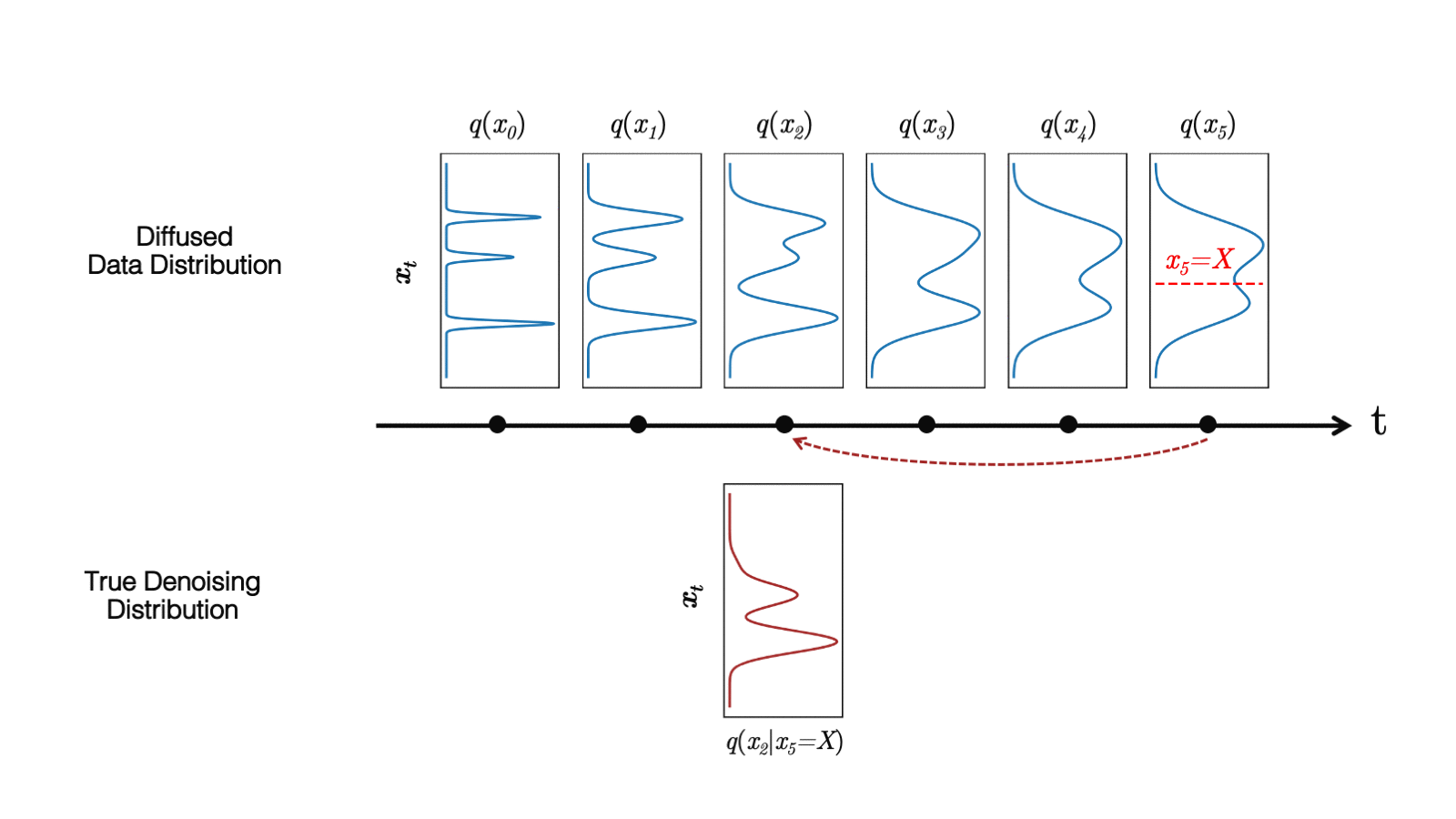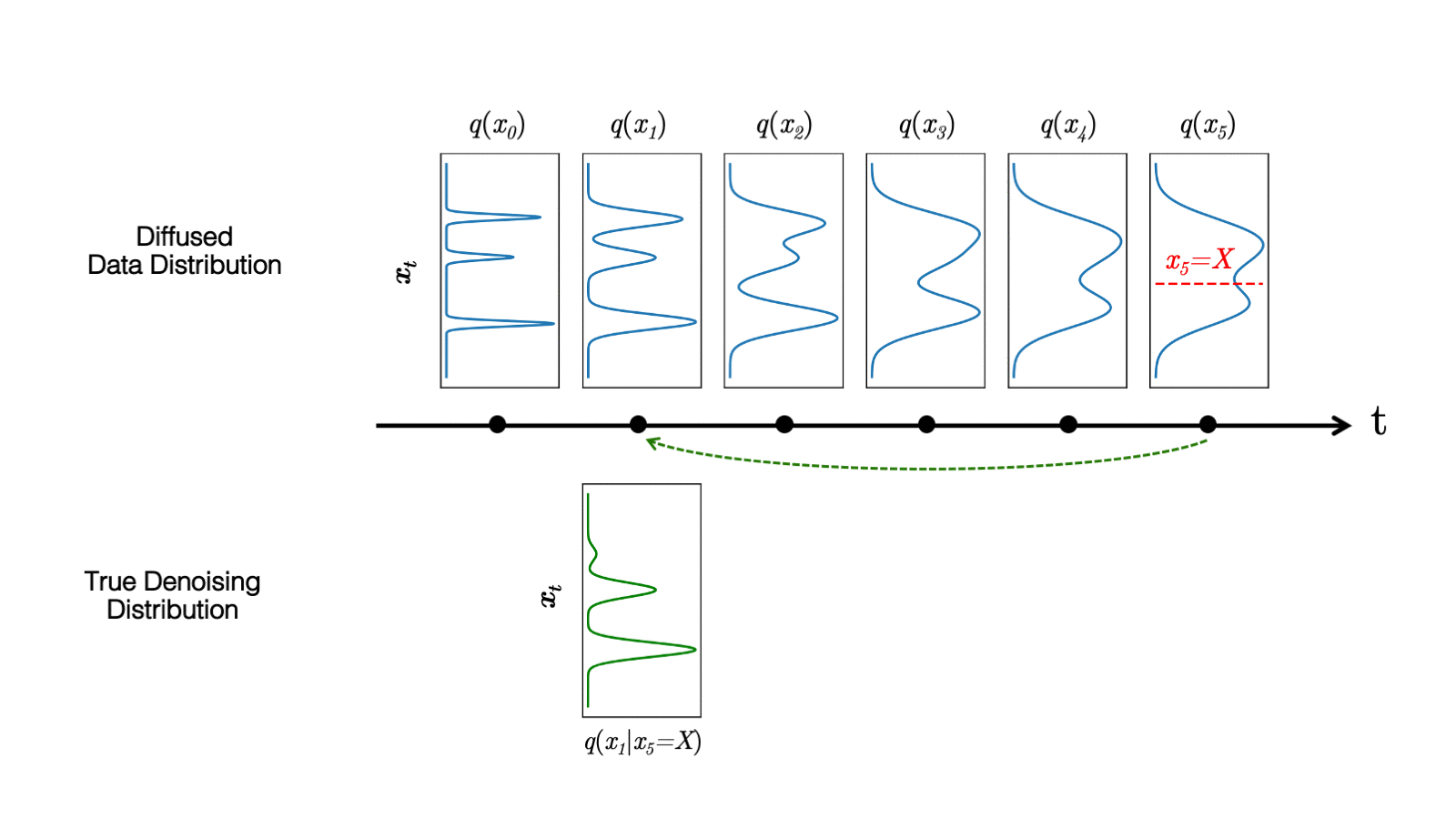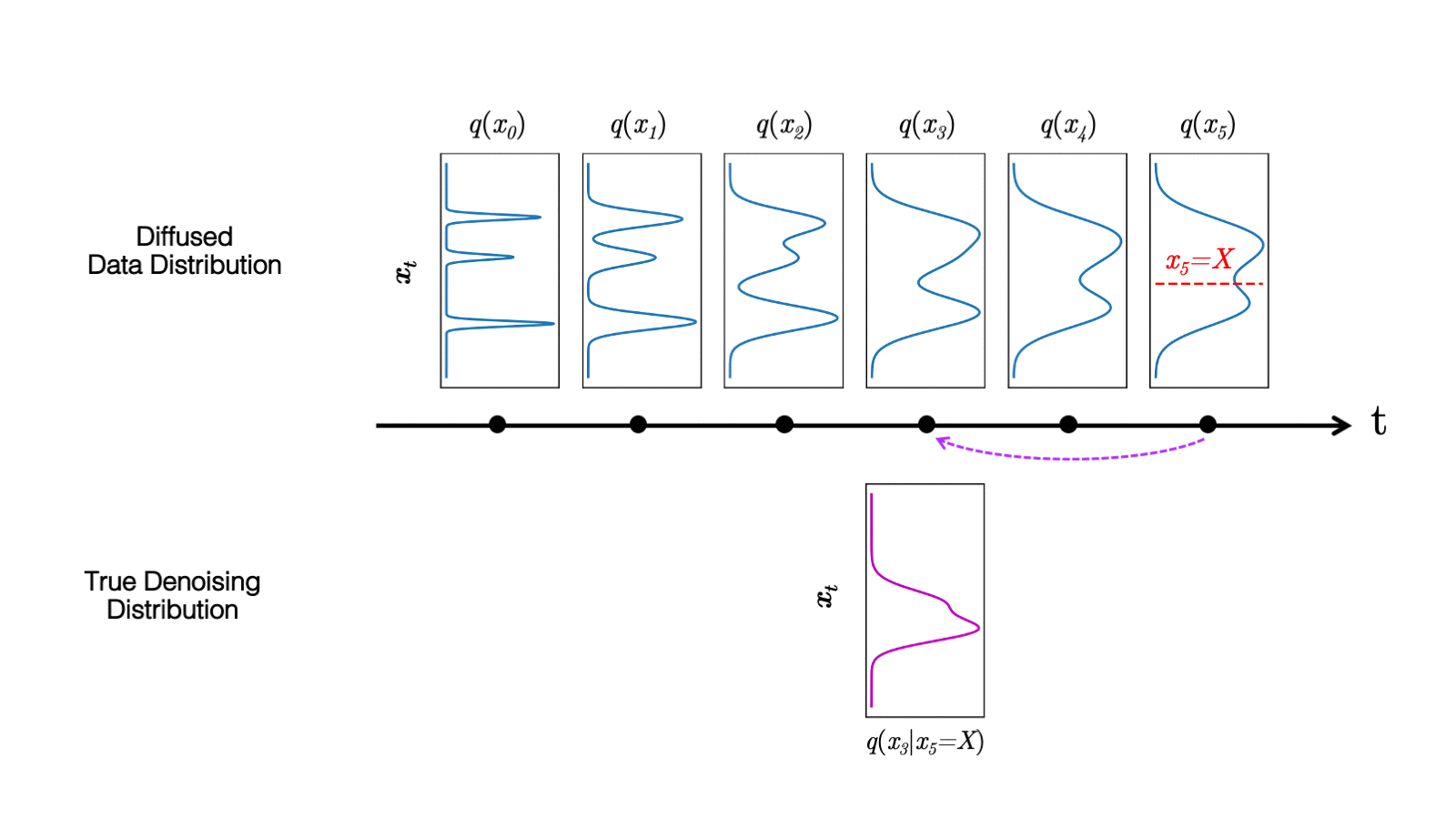
Visualization of diffused 1D data distributions in diffusion models and of the true denoising distributions for different step sizes during denoising. — *Figure 5.* ( 頂部*) 一維數據分布 q （ x ）的演化₀) 根據正向擴散過程。*（下）*在固定 x 軸條件下真實去噪分布的可視化₅以不同的顏色顯示不同的步長。*

在圖 5 中，小步距（以黃色顯示）的真實去噪分布接近高斯分布。然而，隨著步長的增加，它變得更加復雜和多模態。

受上述觀察結果的啟發，我們建議使用表達性多峰分布參數化去噪分布，以實現大步長去噪。特別是，我們引入了一種新的生成模型去噪擴散 GAN ，在該模型中，使用條件 GAN 對去噪分布進行建模（圖 6 ）。

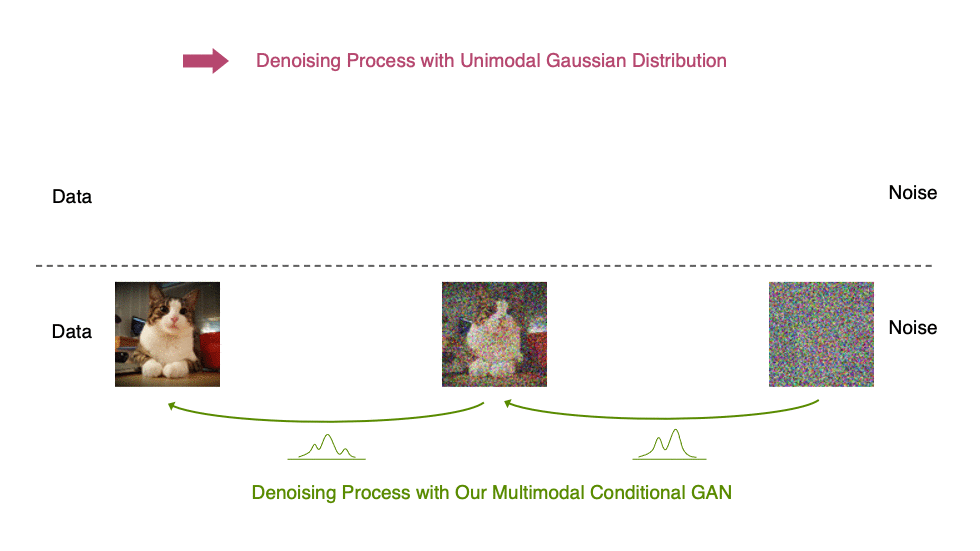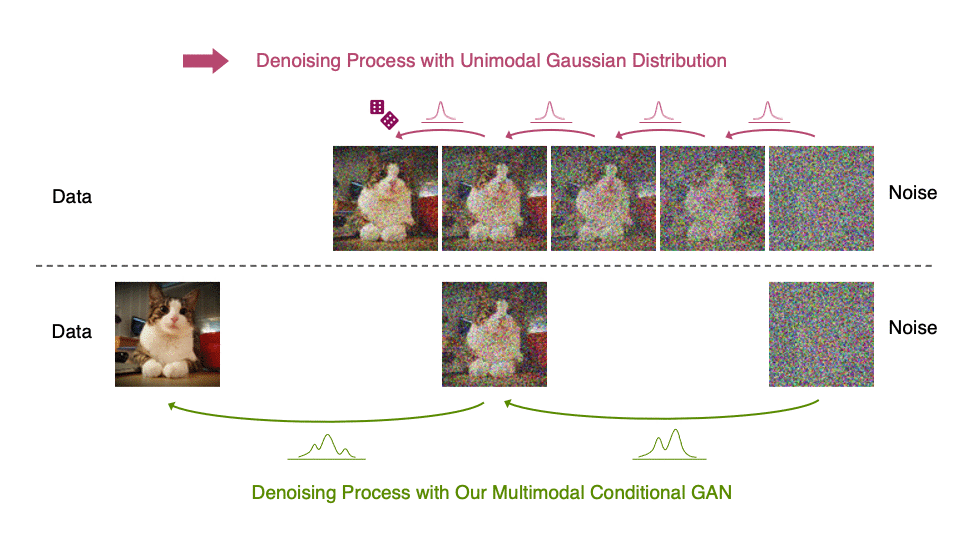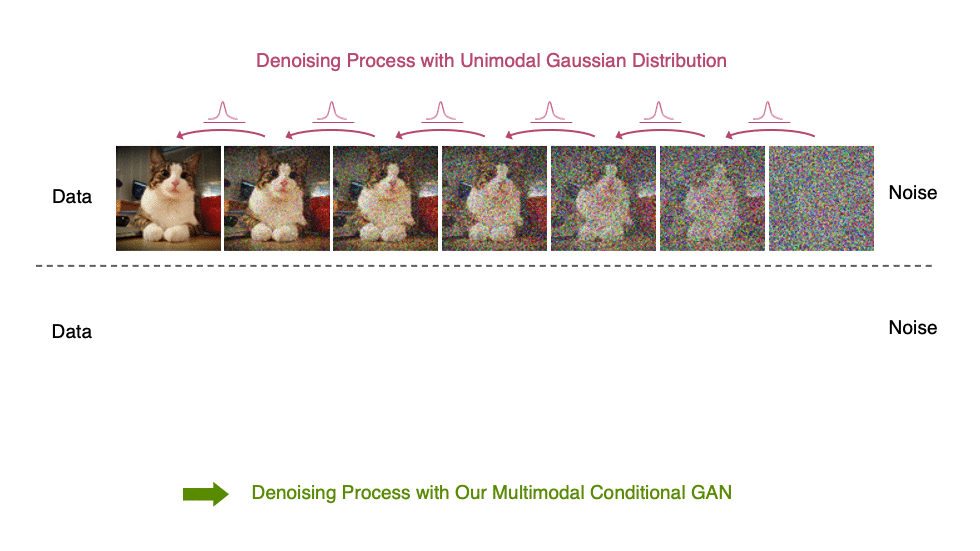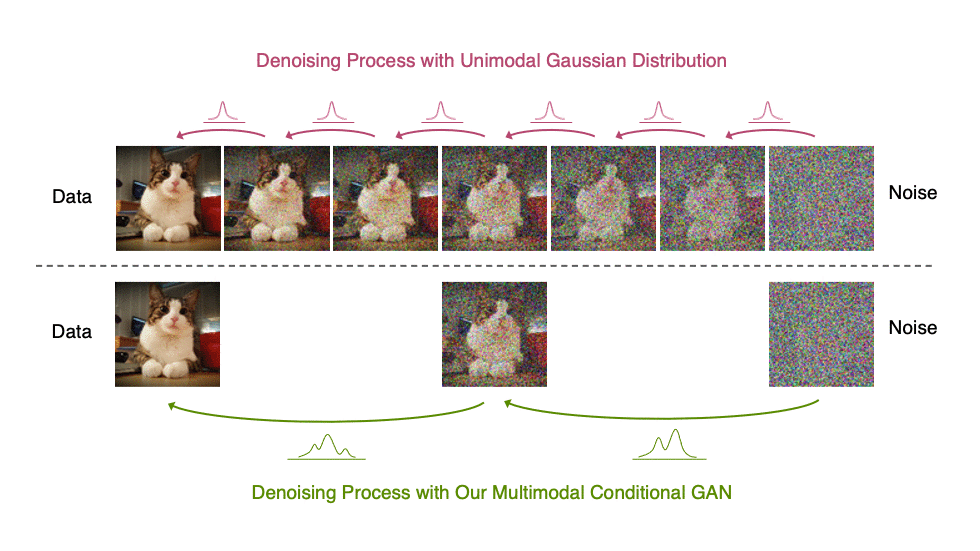
Visualization of the generative denoising process in diffusion models with Gaussian denoising distributions and with Denoising Diffusion GAN. — *圖 6 。去噪擴散過程*

生成性去噪擴散模型通常假設去噪分布可以用高斯分布建模。這一假設僅適用于小的去噪步驟，實際上，這意味著合成過程中有數千個去噪步驟。

在我們的去噪擴散算法中，我們使用多模態和復雜條件算法來表示去噪模型，使我們能夠在兩個步驟中高效地生成數據。

使用對抗性訓練設置對去噪擴散裝置進行訓練（圖 7 ）。給定一個訓練圖像 $\bf{x}0$ ，我們使用前向高斯擴散過程從 $\bf{x}{t-1}$ 和 $\bf{x}_t$ 兩個連續步驟的擴散樣本中取樣。

給定 $\bf{x}t$ ，我們的條件去噪 GAN 首先隨機生成 $\bf{x}'_0$ ，然后使用可處理的后驗分布 $q(\bf{x}'{t-1}|\bf{x}t, \bf{x}'_0)$ 通過加回噪聲生成 $\bf{x}'{t-1}$ 。訓練鑒別器來區分實際 $(\bf{x}{t-1}, \bf{x}_t)$ 和生成的 $(\bf{x}'{t-1}, \bf{x}_t)$ 對，并提供反饋以學習條件去噪算法。

在訓練之后，我們通過從噪聲中采樣并使用我們的去噪擴散生成器在幾個步驟中迭代去噪來生成新實例。

Schematic visualization of the training pipeline of Denoising Diffusion GAN. — *圖 7 。去噪擴散算子的訓練過程* s

我們訓練了一個條件 GAN 發生器，利用擴散過程中不同步驟的對抗性損失對輸入 $x_t$ 進行去噪。

與傳統干草相比的優勢

與我們通過去噪迭代生成樣本的模型相比，為什么不訓練一個可以使用傳統設置一次性生成樣本的 GAN 呢？與傳統的 GaN 相比，我們的模型有幾個優點。

眾所周知， GAN 會遭受訓練不穩定和模式崩潰的影響。一些可能的原因包括難以從復雜分布中一次性直接生成樣本，以及當鑒別器僅查看干凈樣本時存在過度擬合問題。

相比之下，由于 $x_t$ 上的強條件作用，我們的模型將生成過程分解為幾個條件去噪擴散步驟，其中每個步驟對建模相對簡單。擴散過程平滑了數據分布，使鑒別器不太可能過度擬合。

我們觀察到，我們的模型具有更好的訓練穩定性和模式覆蓋率。在圖像生成中，我們觀察到我們的模型實現了與擴散模型競爭的樣本質量和模式覆蓋率，同時只需要兩個去噪步驟。與常規擴散模型相比，它的采樣速度提高了 2000 倍。我們還發現，我們的模型在樣本多樣性方面顯著優于最先進的傳統 GAN ，同時在樣本保真度方面具有競爭力。

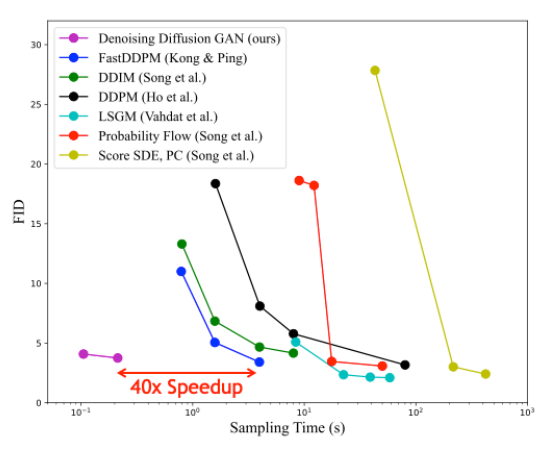
Plot of sample quality vs. sampling time for different denoising diffusion-based generative models. — *圖 8 。基于擴散的不同生成模型的樣本質量與采樣時間*

圖 8 顯示了與 CIFAR-10 圖像建模基準的不同基于擴散的生成模型的采樣時間相比，樣本質量（通過 Fr é chet Inception 距離測量；越低越好）。與其他擴散模型相比，去噪擴散 GaN 在保持相似合成質量的同時實現了幾個數量級的加速。

結論

擴散模型是一類很有前途的深層生成模型，因為它們結合了高質量的合成、強大的多樣性和模式覆蓋。這與常規 GAN 等方法形成對比，后者很受歡迎，但樣本多樣性有限。擴散模型的主要缺點是合成速度慢。

在本文中，我們介紹了 NVIDIA 最近開發的三種技術，它們成功地解決了這一挑戰。有趣的是，他們每個人都從不同的角度處理問題，分析擴散模型的不同組成部分：

潛空間擴散模型基本上簡化了數據本身，首先將其嵌入平滑的潛在空間，在那里可以訓練更有效的擴散模型。
臨界阻尼朗之萬擴散是一種改進的前向擴散過程，特別適合于更簡單、更快的去噪和生成。
擴散算子去噪通過表達性多峰去噪分布，直接學習顯著加速的反向去噪過程。

我們相信，擴散模型非常適合克服生成性學習的三重困境，尤其是在使用本文中強調的技術時。原則上，這些技術也可以結合使用。

事實上，擴散模型已經在深層生成性學習方面取得了重大進展。我們預計，它們可能會在圖像和視頻處理、 3D 內容生成和數字藝術以及語音和語言建模等領域得到實際應用。它們還將用于藥物發現和材料設計等領域，以及其他各種重要應用。我們認為，基于擴散的方法有可能推動下一代領先的生成模型。

最后但并非最不重要的一點是，我們是 2022 年 6 月 19 日在美國路易斯安那州新奧爾良舉行的計算機視覺與模式識別（ CVPR ）會議期間舉辦的擴散模型、其基礎和應用教程組織委員會的成員。如果您對這個主題感興趣，我們邀請您觀看我們的基于去噪擴散的生成建模：基礎與應用教程。

要了解更多關于 NVIDIA 正在推進的研究，請參閱 NVIDIA Research 。

有關擴散模型的更多信息，請參閱以下參考資料：

基于分數的潛在空間生成建模紙張
- 項目頁面： /LSGM GitHub Repo
基于分數的臨界阻尼朗之萬擴散生成模型紙張
- 項目頁面： /CLD-SGM GitHub Repo
用去噪擴散算法解決生成性學習三難問題紙張
- 項目頁面： /denoising-diffusion-gan GitHub Repo

改進擴散模型以替代 GANs ，第 2 部分

潛空間擴散模型

合成速度