DirectX 光線跟蹤中自相交偽影的求解

光線和路徑跟蹤算法通過從攝影機或光源開始并將光線與場景幾何體相交來構建光路。當對象被擊中時，會在這些曲面上生成新的二次光線以繼續路徑。

理論上，這些二次光線不會再次與同一三角形相交，因為相交算法排除了距離為零的相交。然而，在實踐中，實際實現中使用的有限浮點精度往往會導致假陽性結果，稱為自交叉（圖 2）。這會產生偽影，例如陰影痤瘡，其中三角形有時會不正確地陰影自己（圖 1）。

通過使用同一基元的標識符顯式地將其從交集中排除，可以避免自交集。在 DirectX 光線跟蹤（DXR）中，這種自相交檢查將在任何命中著色器中實現。然而，強制任何命中所有三角形命中的調用都會帶來顯著的性能損失。此外，該方法不處理針對相鄰（近）共面三角形的誤報。

解決該問題的最廣泛的方案是使用各種啟發式方法來沿著光線方向或法線偏移光線。然而，這些方法不足以處理各種常見的制作內容，甚至可能需要在每個場景的基礎上手動調整參數，特別是在具有大量平移、縮放或剪切實例化幾何體的場景中。有關詳細信息，請參閱 Ray Tracing Gems: High-Quality and Real-Time Rendering with DXR and Other APIs.

或者，可以在運行時對數值不精確性的來源進行數值限制，從而在交叉測試中給出穩健的誤差區間。然而，這會帶來相當大的性能開銷，并且需要對射線/三角形相交例程的底層實現進行源訪問，這在 DXR 等硬件加速的 API 中是不可能的。

這篇文章描述了一種強大的偏移方法，用于從 DXR 中的三角形派生的二次光線。該方法基于對數值不精確性來源的徹底數值分析。它涉及計算二次光線的生成點，避免自相交。該方法不需要修改遍歷和光線/三角形相交例程，因此可以與 DXR 等閉源和硬件加速的光線跟蹤 API 一起使用。最后，該方法不依賴于使用任意命中著色器的自相交拒絕，并且每個著色點有固定的開銷。

Two renderings of a floating castle. The rendering on the right shows shading artifacts because no self-intersection avoidance is applied. — *圖 1。具有自交叉避免功能（左）和不具有自交叉回避功能（右）的渲染。圖片來源：Sander van der Meiren*

方法概述

二次光線的生成點與入射光線三角形上的命中點重合。目標是計算一個盡可能靠近三角形平面中的命中點的生成點，同時仍然避免自相交。離三角形太近可能會導致自相交偽影，但離得太遠可能會將生成點推過附近的幾何體，從而導致漏光偽影。

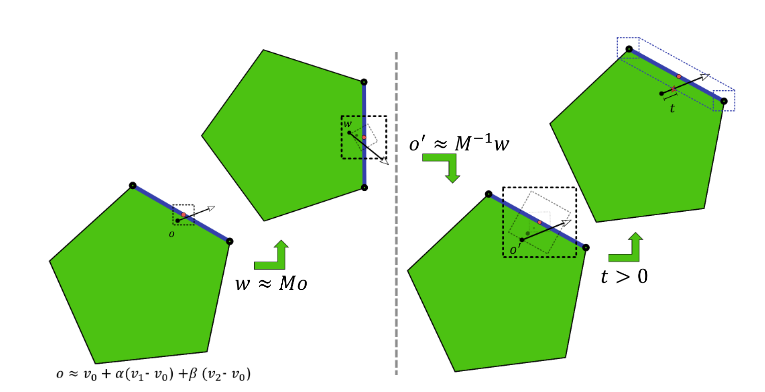
圖 2 顯示了二次射線的數值誤差來源。在用戶著色器中，對象空間的命中點被重建并變換到世界空間中。在 DXR 光線遍歷過程中，世界空間光線將變換回對象空間并與三角形相交。

這些運算中的每一個都會累積數值誤差，可能導致自相交。該方法在每次操作時計算三角形上以預期光線原點（圖 2 中的紅點）為中心的最小不確定性區間。近似射線原點（圖 2 中的黑點）位于該不確定性區間內。光線原點沿三角形法線偏移超過最終不確定性區間，以防止自相交。

A flow diagram of four stages (in green), showing an approximate computed ray origin as it is constructed, transformed, and finally used for a ray-triangle intersection test. — *圖 2:用戶著色器（左）和 DXR 光線遍歷和相交（右）中的數字錯誤源*

命中點

首先在對象空間中重建命中點和幾何三角形法線（清單 1）。

precise float3 edge1 = v1 - v0;
precise float3 edge2 = v2 - v0;

// interpolate triangle using barycentrics
// add in base vertex last to reduce object-space error 
precise float3 objPosition = v0 + mad(barys.x, edge1, mul(barys.y, edge2));
float3 objNormal = cross(edge1, edge2);

通過對三角形頂點進行插值來計算命中點v0，v1,和v2使用 2D 重心命中坐標重錘。雖然可以使用兩個融合的乘加運算來計算插值的命中點，但是添加基頂點v0最后減小了基頂點上的最大舍入誤差，該誤差在實際計算中占主導地位。

使用準確的關鍵字，強制編譯器完全按照指定執行計算。不需要強制精確計算法線和誤差邊界。舍入誤差對這些量的影響微乎其微，可以安全地忽略自交。

接下來，將對象空間的位置轉換為世界空間（清單 2）。

const float3x4 o2w = ObjectToWorld3x4(); 

// transform object-space position
// add in translation last to reduce world-space error
precise float3 wldPosition; 
wldPosition.x = o2w._m03 + 
	mad(o2w._m00, objPosition.x, 
mad(o2w._m01, objPosition.y, 
mul(o2w._m02, objPosition.z ))); 
wldPosition.y = o2w._m13 + 
mad(o2w._m10, objPosition.x, 
mad(o2w._m11, objPosition.y, 
mul(o2w._m12, objPosition.z )));
wldPosition.z = o2w._m23 + 
mad(o2w._m20, objPosition.x , 
mad(o2w._m21, objPosition.y , 
mul(o2w._m22, objPosition.z )));

不使用 HLSL 矩陣 mul 本質，而是寫出變換。這樣可以確保平移部分 ${m_{i,2}}$ 最后添加了轉換的。這再次減少了平移上的舍入誤差，而在實踐中，舍入誤差往往主導該計算中的誤差。

最后，將對象空間法線轉換為世界空間，并對其進行規范化（清單 3）。

const float3x4 w2o = WorldToObject3x4();

// transform normal to world-space using 
// inverse transpose matrix
float3 wldNormal = mul(transpose((float3x3)w2o), objNormal); 

// normalize world-space normal
const float wldScale = rsqrt(dot(wldNormal, wldNormal)); 
wldNormal = mul(wldScale, wldNormal);

// flip towards incoming ray 
if(dot(WorldRayDirection(), wldNormal) > 0) 
wldNormal = -wldNormal;

若要支持具有不均勻縮放或剪切的變換，法線將使用反向轉置變換進行變換。在變換之前不需要規范化對象空間法線。無論如何，有必要在世界空間中再次正常化。由于稍后需要再次使用世界法線的反向長度來適當縮放誤差邊界，因此手動進行歸一化，而不是使用 HLSL規范化固有的

錯誤界限

使用近似的世界空間位置和三角形法線，繼續計算計算位置的誤差邊界，邊界為最大有限精度舍入誤差。有必要考慮清單 1 和 2 中計算中的舍入誤差。

還需要考慮遍歷過程中可能出現的舍入錯誤（圖 2）。在遍歷過程中，DXR 將應用世界到對象的變換并執行射線三角形相交測試。這兩者都是以有限精度執行的，因此會引入舍入誤差。

首先計算一個組合的對象空間誤差邊界，同時考慮清單 1 中的舍入誤差和 DXR 射線三角形相交測試引起的舍入誤差（清單 4）。

const float c0 = 5.9604644775390625E-8f;
const float c1 = 1.788139769587360206060111522674560546875E-7f; 
 
// compute twice the maximum extent of the triangle 
const float3 extent3 = abs(edge1) + abs(edge2) + 
   abs(abs(edge1) - abs(edge2)); 
const float extent = max(max(extent3.x, extent3.y), extent3.z); 
 
// bound object-space error due to reconstruction and intersection 
float3 objErr = mad(c0, abs(v0), mul(c1, extent));

請注意，三角形交點上的誤差受沿三維的最大三角形范圍的限制。這一界限的嚴格證明超出了本文的范圍。為了提供直觀的對正，在執行相交測試之前，常見的光線三角形相交算法將三角形重定向到“光線空間”（通過減去光線原點）。在自相交的上下文中，光線原點位于三角形上。因此，該光線空間中剩余三角形頂點的大小由三角形沿每個維度的范圍限定。

此外，這些相交算法將三角形投影到 2D 平面中。此投影會導致沿一個維度的誤差擴散到其他維度。因此，取沿所有維度的最大范圍，而不是單獨處理沿維度的誤差。射線三角形相交測試的精確邊界將是硬件特定的。常數c1針對 NVIDIA RTX 硬件進行了調整，但可能需要在不同平臺上進行一些調整。

自定義相交基本體的錯誤邊界取決于其相交著色器的實現細節。想要深入了解有限精度舍入誤差的分析，請參閱 Advanced Linear Algebra: Foundations to Frontiers。

接下來，計算由于命中點從對象空間到世界空間的轉換而導致的世界空間誤差界限（清單 5）。

// bound world-space error due to object-to-world transform 
const float c2 = 1.19209317972490680404007434844970703125E-7f; 
float3 wldErr = mad(c1, mul(abs((float3x3)o2w), abs(objPosition)), 		
     mul(c2, abs(transpose(o2w[3]))));

這就留下了 DXR 在光線遍歷過程中執行的從世界到對象變換的舍入錯誤（清單 6）。

// bound object-space error due to world-to-object transform 
objErr = mad(c2, mul(abs(w2o), float4(abs(wldPosition), 1)), objErr);

與射線三角形相交測試一樣，世界到對象變換中的舍入誤差取決于硬件。常數c2是保守的，并且應該足以用于實現向量矩陣乘法的各種方式。

世界到對象變換矩陣及其逆的有限精度表示不能保證精確匹配。在分析中，表示中的錯誤可以歸因于其中之一。由于對象到世界的轉換是在用戶代碼中執行的，因此錯誤最好歸因于對象到世界轉換矩陣，從而實現更嚴格的邊界。

抵消

上一節解釋了如何計算二次光線構造和遍歷的舍入誤差的邊界。這些邊界在近似的、有限精度的射線原點周圍產生一個區間。預期的、全精度的“真實”射線原點保證位于該區間的某個位置。

真正的三角形通過真正的光線原點，所以三角形也通過這個區間。圖 3 顯示了如何沿三角形法線偏移近似原點，以確保其位于真實三角形之上，從而防止自相交。

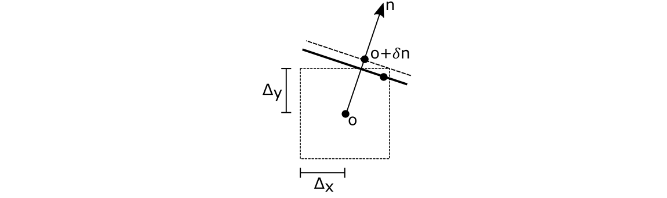
The approximate computed ray origin, centered inside a 2D uncertainty interval. The true ray origin lies within the uncertainty interval. The true triangle passing through the true ray origin. The triangle normal, passing through the approximate ray origin and a conservatively offset triangle, touching the uncertainty interval. The offset ray origin is the intersection of the triangle normal and the conservatively offset triangle. — *圖 3。通過將光線原點沿法線偏移到誤差間隔之外來避免自相交*

將誤差界?投影到法線 n 上，以獲得沿法線的偏移δ

${\delta = \frac{\Delta \cdot {abs}\left(n\right)}{n \cdot n}}$

法線上的舍入誤差與誤差邊界和偏移本身計算上的舍入錯誤具有相似的大小。這些都是微不足道的，在實踐中可以忽略不計。將對象和世界空間偏移合并為沿世界空間法線的單個世界空間偏移（清單 7）。

// compute world-space self-intersection avoidance offset 
float objOffset = dot(objErr, abs(objNormal)); 
float wldOffset = dot(wldErr, abs(wldNormal)); 

wldOffset = mad(wldScale, objOffset, wldOffset);

使用已規范化的世界空間法線 ${\bar{n}_w}$ 來自清單 3。世界空間偏移 ${\delta_w}$ 簡化為 $\delta_w = \Delta \cdot {abs}\left( \bar{n}_w \right)$ .對象空間偏移 ${\delta_o}$ 沿著對象空間法線 ${n_o}$ 需要轉化為世界空間 ${\delta_o M n_o}$ 。

但是，請注意，變換后的對象空間偏移不一定平行于世界空間法線 ${n_w}$ 。若要獲得沿世界空間法線的單個組合偏移，請將變換后的對象空間偏移投影到世界空間法線上，如 ${\delta_o M n_o \cdot n_w}$ .使用 ${n_w = M^{-T} n_o}$ 這簡化為：

${\delta_o M n_o \cdot M^{-T} n_o = \delta_o \left( M n_o \right)^T M^{-T} n_o = \delta_o n_o \cdot M^T M^{-T} n_o = \delta_o n_o \cdot n_o = \Delta \cdot {abs}\left(n\right)}$

最后，使用計算出的偏移量沿著三角形法線擾動命中點（清單 8）。

// offset along the normal on either side. 
precise float3 wldFront = mad( wldOffset, wldNormal, wldPosition);
precise float3 wldBack  = mad(-wldOffset, wldNormal, wldPosition);

這就產生了前面和后面的產卵點，它們不會發生自交叉。導出的誤差邊界（以及偏移）既不取決于入射光線方向，也不取決于出射二次光線方向。因此，可以對源自該命中點的所有次級光線重復使用相同的生成點。所有反射光線都應該使用前生成點，而透射光線應該使用后生成點。

方向的對象到世界和世界到對象變換也會導致光線方向上的舍入誤差。在極端的掠角下，這些舍入誤差可能會導致它翻轉，將其定向回三角形。這篇文章中的抵消方法并不能防止這種舍入誤差。通常建議濾掉極端角度的二次光線。

或者，可以在光線方向變換上導出類似的誤差邊界。然后，沿三角形法線偏移光線方向（對于光線原點）可以保證其側性。然而，由于常見 BRDF 模型的反射率分布在掠入射角處趨于零，因此在許多應用中可以安全地忽略這個問題。

對象空間

如清單 4 所示，偏移量在對象空間中的三角形范圍和三角形底頂點的大小中線性增長。對于小三角形，底頂點的舍入誤差將主導對象空間誤差（圖 2）。因此，可以通過在對象空間中重新定位幾何體，使其圍繞對象空間原點居中，以最小化到原點的距離，來減少對象空間誤差。對于具有超大三角形的幾何體（如地平面），可能值得對幾何體進行鑲嵌，并進一步減少三角形范圍中的舍入誤差。

攝像頭空間

如清單 5 和 6 所示，偏移量的大小將隨著世界空間位置的大小線性增長。比例常數c2約為 1 ulps。遠處的實例化幾何體 ${d}$ 來自世界空間中場景原點的最大舍入誤差為 ${d2^{-22}}$ ，或每 4 公里偏移 1 毫米。偏移量也與三角形范圍和對象空間位置成線性比例。

對于圖 4 中的一個例子，在距離世界空間原點 1 公里的 20 米（物體空間原點在根部）的樹上，在 10 厘米的葉子上產生的二次射線，由于三角形范圍、物體空間位置和世界空間位置，偏移幅度將分別為 45 納米、4μm 和 0.25 毫米。在實踐中，? 世界空間位置中的舍入誤差往往主導所有舍入誤差。對于相對較小對象的大型場景尤其如此。

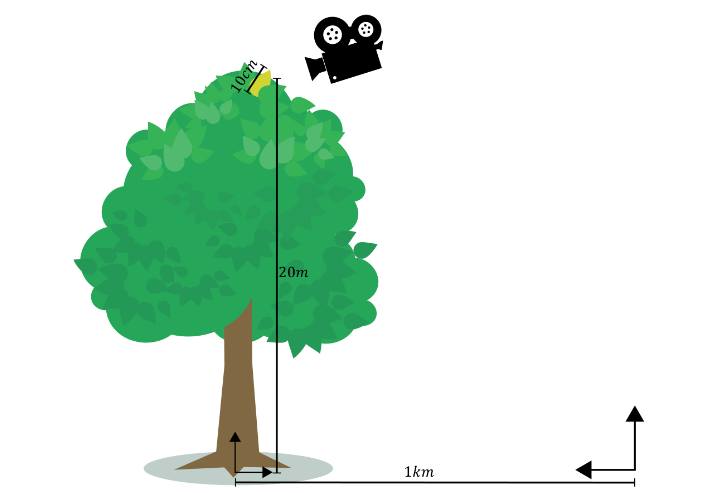
A diagram of a tree, placed 1 km from the world-space scene origin. Measurements are shown for a leaf of 10 cm within the tree, placed 20 m from the object-space origin. A camera icon is close to the tree, oriented towards the leaf. — *圖 4。偏移幅度與三角形范圍、對象空間位置和世界空間位置幅度成線性關系*

請注意，誤差與到場景原點的世界空間距離成比例，而不是與場景攝影機成比例。因此，如果攝影機遠離場景原點，則從附近幾何體產生的光線的偏移可能會變得過大，導致視覺偽影。

可以通過將整個場景轉換到攝影機空間來減少此問題。所有實例都將重新定位，以便攝影機原點與世界空間原點重合。因此 ${d}$ 變為該相機空間中到相機的距離，并且偏移幅度將與到相機的間距成比例。從攝影機附近的幾何體產生的光線將享受相對較小的偏移，從而降低由于偏移而產生視覺偽影的可能性。

連接射線

到目前為止，討論的重點是偏移光線原點，以防止原點處的自相交。光線和路徑跟蹤算法還跟蹤光線，以評估不同三角形上兩點之間的可見性，例如連接著色點和光源的陰影光線。

這些光線可能在光線的任一端發生自相交。有必要偏移兩端以避免自相交。端點的偏移以與光線原點類似的方式計算，但使用對象到世界和世界到對象的變換矩陣、端點的重心和三角形頂點，并使用連接光線方向作為入射光線方向。

與散射光線相反，有必要考慮世界中的舍入誤差，以在遍歷過程中進行對象光線方向變換。從理論上講，在射線三角形相交測試中也有必要考慮額外的舍入誤差，因為射線原點不在端點三角形上。然而，這個額外的誤差與世界到對象的誤差成亞線性，因此為了簡單起見，這些誤差被隱式地組合在一起。

對于端點，清單 6 中的世界到對象轉換錯誤計算被替換為（清單 9）。

// connection ray direction 
precise float3 wldDir = wldEndPosition - wldOrigin; 
 
// bound endpoint object-space error due to object-to-world transform 
float4 absOriginDir = (float4)(abs(wldOrigin) + abs(wldDir), 1); 
objEndErr = mad(c2, mul(abs(w2oEnd), absOriginDir), objEndErr);

在這里wld 原點是世界空間中的連接射線原點。在 DXR 中，射線是使用原點和方向定義的。將偏移直接應用于世界空間方向，而不是偏移端點并重新計算光線方向。對于端點偏移，清單 8 就變成了清單 10。

// offset ray direction along the endpoint normal towards the ray origin 
wldDir = mad(wldEndOffset, wldEndNormal, wldDir) ; 
 
// shorten the ray tmax by 1 ulp 
const float tmax = 0.99999994039f;

將光線長度縮短 1 ulp，以考慮方向計算中的舍入誤差。

在實踐中，使用廉價的近似偏移啟發式方法與基于標識符的自相交拒絕相結合的更簡單方法通常足以避免端點自相交。近似偏移將避免大多數端點自相交，而基于標識符的命中拒絕將照顧剩余的自相交。

對于二次散射光線，請避免基于標識符的自相交拒絕，因為這需要為光線上的每個相交調用任意命中著色器，從而增加顯著的性能開銷。然而，對于可見性光線，基于端點標識符的命中拒絕的額外性能開銷是最小的。

對于使用RAY_FLAG_ACCEPT_FIRST_HIT_AND_END_SEARCH標志時，最多會有兩個額外的報告命中：被拒絕的端點自交叉和任何阻塞終止遍歷。

對于不使用RAY_FLAG_ACCEPT_FIRST_HIT_AND_END_SEARCH標志，自相交可以在最近命中著色器中拒絕，而不是在任何命中著色器中。如果可見性光線調用端點三角形的最近命中著色器，則未找到更近的命中，因此該命中應簡單地視為最近命中著色器中的未命中。

結論

本文提出的方法為二次光線的自相交提供了一個穩健且易于使用的解決方案。該方法應用最小的保守偏移，解決了自相交偽影，同時減少了漏光偽影。此外，該方法具有最小的運行時開銷，并且易于在常見的著色管道中集成。雖然這篇文章描述了 DXR 的 HLSL 實現，但該方法很容易轉換為 Vulkan 的 GLSL 和 OptiX 的 CUDA 。

想要獲取更多信息，請訪問 NVIDIA/self-intersection-avoidance 在 GitHub 上查看 HLSL 和 GLSL 示例實現。同時，您也可以查看 OptiX Toolkit ShaderUtil Library，這是一個用于自交叉避免的現成 OptiX 頭庫。

DirectX 光線跟蹤中自相交偽影的求解

方法概述

命中點

錯誤界限

抵消

對象空間

攝像頭空間

連接射線

結論

相關資源

標簽

關于作者

DirectX 光線跟蹤中自相交偽影的求解

方法概述

命中點

錯誤界限

抵消

對象空間

攝像頭空間

連接射線

結論

相關資源

標簽

關于作者

相關文章

NVIDIA OptiX 著色器綁定表優化實現高效光線追蹤

相關文章

首個設備上小語言模型的部署提高游戲角色扮演體驗

NVIDIA Nsight Graphics 幫助您輕松調試著色器

使用深度學習框架 fVDB 根據真實的 3D 數據構建空間智能

利用 NVIDIA Kaolin 庫模擬任何表示下的彈性物體

Differential Slang：應用實例